Квадратичная функция (парабола)

Квадратичная функция - это функция, заданная формулой вида $у = ах^2 + bх + с$, где х - аргумент, $a, b, c \in \mathbb{R} , a \neq 0$.

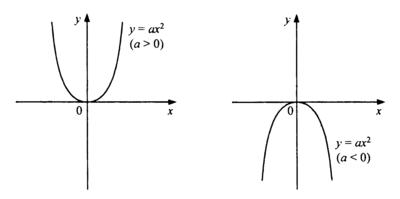
Рассмотрим функцию, заданную формулой $у = ах^2 (a\neq 0)$.

Квадратичная функция (парабола)

Свойства функции $y = ах^2$:

  1. Если x=0, то y=0, то есть график функции проходит через начало координат.
  2. Если x\neq 0, то у>0 при а>0 и у<0 при а<0.
  3. График функции симметричен относительно оси y.
  4. При а>0 функция убывает на промежутке $(-\infty;\; 0]$ и возрастает на промежутке $[0;\; +\infty)$; при a<0 функция возрастает на промежутке $(-\infty;\;0]$ и убывает на промежутке $[0;\; +\infty)$.
  5. При $а>0\,y_{мин} = 0\text{ , при }а<0\,y_{макс} = 0$.

График функции $у = ах^2 + n$ получается из графика функции $у = ах^2$ параллельным переносом вдоль оси y на n единиц вверх при n>0 или на (-n) единиц вниз, если n<0.

График функции $y = a(x-m)^2$ получается из графика функции $у = ах^2$ параллельным переносом вдоль оси x на m единиц вправо при m>0 или на (-m) единиц влево, если m<0.

Вершина параболы - это точка пересечения параболы с её осью симметрии.

Вершина параболы $y = ax^2 + bx + c$ имеет координаты $(-\frac{b}{2a}\;;\;\frac{b^2-4ac}{4a})$.

Пример 1. На рисунке изображён график квадратичной функции y=f(x). график квадратичной функции y=f(x) 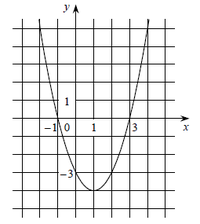Какие из следующих утверждений о данной функции неверны? Запишите их номера.

  1. Функция убывает на промежутке [1; +∞) .
  2. Наименьшее значение функции равно −4 .
  3. f(−2) < f(3) .

Видео-решение.