Определение перемещений в рамах
Видео урок 1:Определение перемещений в рамах .
Видео урок 1:Определение перемещений в рамах .
Задача 1
Найти линейное и угловое перемещения точки A на конце гэобразной консольной рамы, у которой жесткость стойки вдвое больше жесткости ригеля (рис. а).
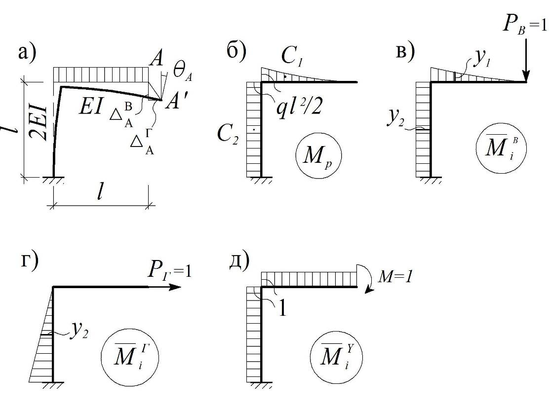Рис 3-15 с55
Решение.
Строим эпюру Mp от заданной нагрузки и эпюры Mi от единичных сил и моментов, приложенных в точке A (рис. б-д).
Определяем вертикальное перемещение точки А, перемножая эпюры Mp и M в:
в = (Mp M в) = (1/EJ) w1 y1 + (1/2EJ) w2 y2 = (1/EJ)(1/3)l (ql2/2)(3/4)l + + (1/2EJ) l(ql2/2)l = (3/8)(ql4/EJ).
Находим горизонтальное перемещение точки А:
г = (Mp M г) = (1/2EJ) l(ql2/2)(l/2) = (1/8)(ql4/EJ).
Полное перемещение точки А составит:
___________ __
А = (в)2 + (г)2 = (10 ql4)/8EJ.
Угол поворота сечения в точке А будет равен:
А = (Mp M у) = (1/EJ) w1×1 + + (1/2EJ) w2×1 = (1/EJ)(1/3)l (ql2/2)1 + + (1/2EJ) l(ql2/2)1 = (5ql3/12EJ ).
Рассмотренный пример наглядно показывает, почему при определении перемещений в рамах мы пренебрегаем продольными деформациями.
Верти-кальное перемещение точки А от заданной нагрузки в основном определяется изгибом ригеля, изгибом стойки и только в очень незначительной степени – ее сжатием.