Метод сил

Видео урок 1:Метод сил .

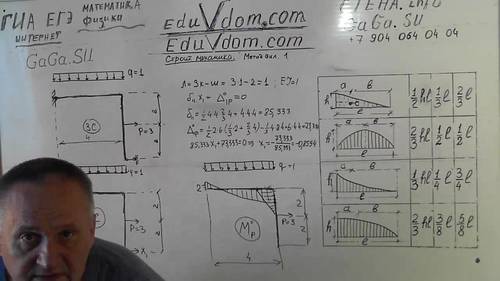
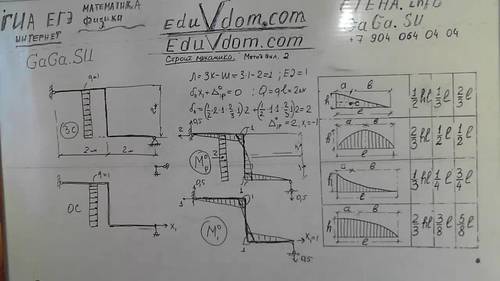
Видео урок 2:Метод сил .

Основная идея метода сил очень проста и может быть рассмотрена на следующем примере. 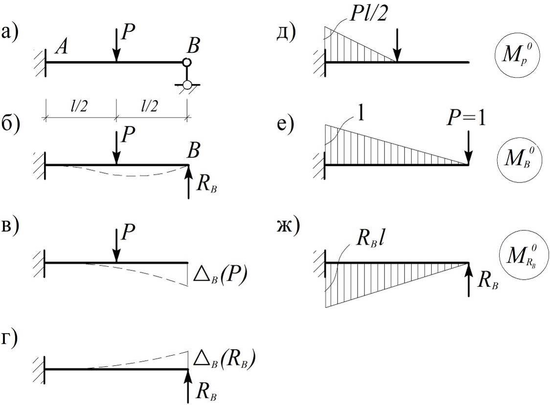Определить реакцию Rв статически неопределимой балки от заданной нагрузки, полагая ее жесткость равной EJ (рис. а).

Они справедливы не только для рам, но и для любых статически неопределимых стержневых систем.

Каждое из уравнений этой системы имеет геометрический смысл – оно выражает отсутствие перемещения в основной системе в направлении

отброшенной лишней связи.

В качестве неизвестных выступают силы: $ X_{1},X_{2},\ldots,X_{n}, $, откуда – название метода.

Для n неизвестных систему канонических уравнений МС можно записать в следующем виде: $$ \sum _{j=1}^{n}\delta _{ij}X_{j}+\Delta _{ip}^{0}=0, \left ( i=1,2,\ldots,n \right ) $$

$$ \delta _{ij}=\delta _{ji} $$

Решив эту систему уравнений и определив неизвестные $ X_{1},X_{2},\ldots,X_{n}, $ мы сведем дальнейший расчет СНС к расчету статически определимой

основной системы, загруженной заданной нагрузкой и найденными реакциями дополнительных связей.

Пример 1

Определить опорные реакции рамы (рис. а), полагая жесткость EJ

постоянной.

Решение.

1) Определяем число лишних связей системы: Л = 3К – Ш = 3.1 – 1 = 2

и выбираем основную систему, отбрасывая две линейные связи шарнира В и заменяя их неизвестными реакциями $ X_{1} $ и $ X_{2} $ (рис. б).

Система канонических уравнений для данной системы примет вид: $$ \delta _{11}X_{1}+\delta _{12}X_{2}+\Delta _{1p}^{0}=0 $$ $$ \delta _{21}X_{1}+\delta _{22}X_{2}+\Delta _{2p}^{0}=0 $$

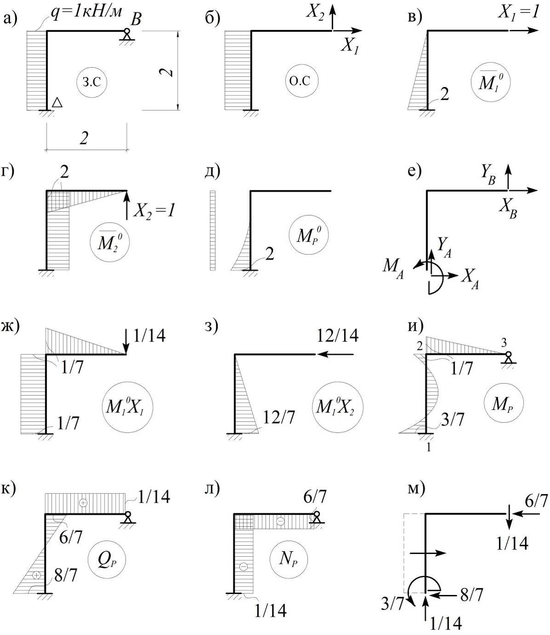
2) Строим эпюры изгибающих моментов от единичных значений неизвестных и от заданной нагрузки в основной системе (рис. в-д).

3) Вычисляем коэффициенты и свободные члены Система канонических уравнений $$ \delta _{11}=\frac{8}{3EJ} $$ $$ \delta _{12}=-\frac{4}{EI} $$ $$ \delta _{22}=\frac{32}{3EI} $$ $$ \Delta _{1p}^{0}=\frac{2}{EI} $$ $$ \Delta _{2p}^{0}=-\frac{8}{3EI} $$

4) Решая систему канонических уравнений : $$ \left ( \frac{8}{3} \right )X_{1}-4X_{2}=-2 $$ $$ -4X_{1}+\left ( \frac{32}{3} \right )X_{2}=\frac{8}{3} $$

находим: $$ X_{1}=-\frac{12}{14}kH $$ $$ X_{2}=-\frac{1}{14}kH $$

5) Определяем опорные реакции основной системы от одновременного действия распределенной нагрузки и найденных неизвестных: $$ \sum M_{A}=0 $$ $$ \sum X=0 $$ $$ \sum Y=0 $$ $$ M_{A}=\frac{3}{7}kHм $$ $$ X_{A}=-\frac{8}{7}kH $$ $$ Y_{A}=\frac{2}{7}kH $$

Одновременно эти реакции вместе с найденными ранее $ X_{1} $ и $ X_{2} $ дают ответ на вопрос, чему равны опорные реакции

заданной статически неопределимой рамы (рис. е): $$ M_{A}=\frac{3}{7}kHм $$ $$ X_{A}=-\frac{8}{7}kH $$ $$ Y_{A}=\frac{2}{7}kH $$ $$ X_{B}=-\frac{6}{7}kH $$ $$ X_{B}=-\frac{1}{14}kH $$

Пример 2

Построить эпюры внутренних усилий для заданной рамы (рис. а).

Решение.

1) Находим изгибающие моменты по формуле: $$ M_{p}=\bar{M_{1}^{0}}X_{1}+\bar{M_{2}^{0}}X_{2} $$

воспользовавшись найденными ранее значениями $ X_{1} $ и $ X_{2} $ – см. пример 1.

На ригеле эта эпюра совпадает с эпюрой $ \bar{M_{1}^{0}}X_{1} $(рис. ж), поскольку на

этом участке эпюры $ \bar{M_{p}^{0}} $ и $ \bar{M_{2}^{0}} $ равны нулю.

Для построения $ M_{p} $ на стойке достаточно вычислить ее значения в 1-ом

узле (рис. и):

$$ M_{1}=2+\frac{1}{7}-\frac{12}{7}=\frac{3}{7}kHм $$

2) При построении эпюры на стойке будем, для определенности, считать

первый узел – левым, а второй – правым.

Тогда получим: $$ Q_{12}=\frac{ql_{12}}{2}+\left ( M^{пр}-M^{лев} \ )\right/l_{12}=\left ( 1\cdot 2 \right )/2+\left ( -1/7-\left ( -3/7 \right ) \right )/2=1+1/7=8/7 $$ $$ Q_{21}=\frac{ql_{12}}{2}+\left ( M^{пр}-M^{лев} )\right/l_{12}=-1+1/7=6/7 $$

На ригеле местная нагрузка отсутствует, поэтому (рис. к): $$ Q_{23}=Q_{32}=\left ( 1/7 \right )/2=1/14kH $$

3) Для построения эпюры Np достаточно рассмотреть равновесие 2-го узла

рамы: $$ \sum X=0; N_{23}=-Q_{21}=-6/7kH $$ $$ \sum Y=0; N_{21}=-Q_{23}=-1/14kH $$

Для проверки правильности построения эпюр можно рассмотреть равновесие

части рамы (рис. м), расположенной выше сечения, проведенного вблизи опор A и B – где известны значения всех трех эпюр: $$ \sum X=2-6/7-8/7=0 $$ $$ \sum Y=2/7-8/7=0 $$ $$ \sum M_{A}=3/7-2\cdot 1+\left ( 6/7 \right )\cdot 2-\left ( 1/14 \right )\cdot 2=0 $$