Графическое определение равнодействующей сходящихся сил

Теорема 1. Равнодействующая системы сходящихся сил существует, приложена в центре системы, равна их геометрической (векторной) сумме и изображается замыкающей стороной силового многоугольника.

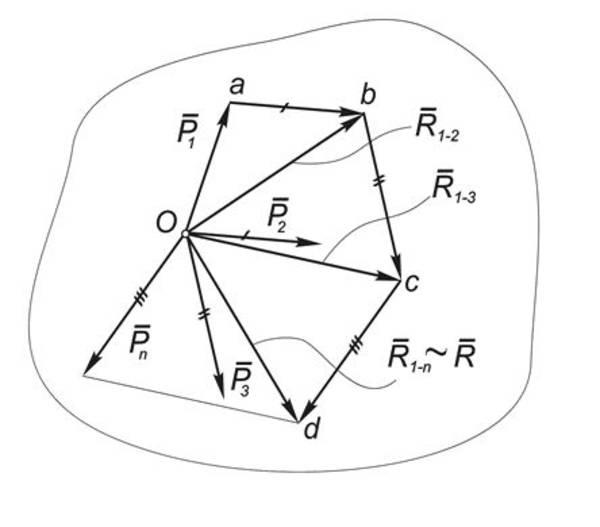
Для доказательства рассмотрим систему сходящихся сил, приложенных в центре О : (Рис.1).

По аксиоме параллелограмма две первых силы этой системы можно заменить равнодействующей $\vec{R_{1-2}}$, которая изображается замыкающей стороной силового треугольника Oab и как вектор равна сумме векторов $\vec{Р_1}$ и $\vec{Р_2}$:

$$(\vec{Р_1}, \vec{Р_2}) \sim ( \vec{R_{1-2}} = \vec{Р_1} + \vec{Р_2}$$

Затем точно так же можно найти равнодействующую силы $\vec{R_{1-2}}$ и силы $\vec{Р_3}$, откладывая от точки b вектор $bc = \vec{Р_3}$:

$$(\vec{Р_1}, \vec{Р_2}, \vec{Р_3}) \sim (\vec{R_{1-2}}, \vec{Р_3}) \sim \vec{R_{1-3}} = \vec{Р_1} + \vec{Р_2} + \vec{Р_3}$$

Продолжая эту процедуру, мы найдем равнодействующую всей системы:

$$(\vec{Р_1}, \vec{Р_2}, \dots, \vec{Р_n}) \sim (\vec{R_{1-(n-1)}} , \vec{Рn}) \sim (\vec{R_{1-n}}) \sim \vec{R} = \sum_{i=1}^{i=n} \vec{Р_i}$$

, которая изображается замыкающей стороной силового многоугольника Oabcd.

Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.

Универсальным для определения равнодействующей системы сходящихся сил является аналитический метод, к рассмотрению которого мы и переходим.

• Результат графического определения равнодействующей не изменится, если силы суммировать в другой последовательности, хотя при этом мы получим другой силовой многоугольник – отличный от первого.
• Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.