Сложение пар сил

Теорема 1. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре с вектор-моментом, равным геометрической сумме вектор-моментов слагаемых пар.

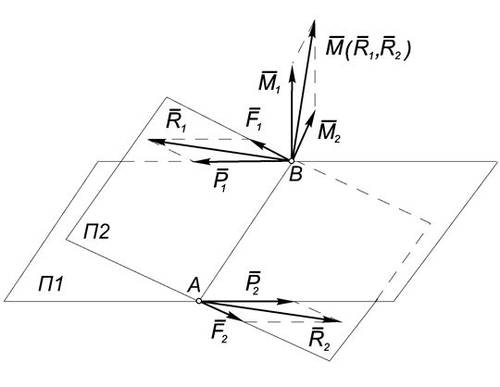
Для доказательства рассмотрим две пары сил $(\vec{P_1}, \vec{P_2})$ и $(\vec{F_1}, \vec{F_2})$, лежащие в плоскостях П₁ и П₂ соответственно, которые пересекаются по прямой АВ.

Не уменьшая общности можно считать, что плечи этих пар равны отрезку АВ этой прямой. Пусть $\vec{M}(\vec{P_1},\, \vec{P_2}) = \vec{M_1}$ , а $\vec{M}(\vec{F_1}, \vec{F_2}) = \vec{M_2}$ (Рис.1) .

Рис.1

Воспользовавшись аксиомой параллелограмма, получим:

$$((\vec{P_1}, \vec{P_2}), (\vec{F_1}, \vec{F_2})) \sim ((\vec{P_1}, \vec{F_1}), (\vec{P_2}, \vec{F_2})) \sim (\vec{R_1}, \vec{R_2})$$

При этом момент результирующей пары с учетом теоремы Вариньона будет равен:

$$\vec{M}(\vec{R_1}, \vec{R_2}) = \vec{M_A}(\vec{R_1}) = \vec{M_A}(\vec{P_1}) + \vec{M_A}(\vec{F_1}) = \vec{M}(\vec{P_1}, \vec{P_2}) + \vec{M}(\vec{F_1}, \vec{F_2}) = \vec{M_1} + \vec{M_2}$$

Теорема доказана.

Следствия:

1. Система n пар в пространстве эквивалентна одной паре с вектор-моментом, равным геометрической сумме вектор-моментов слагаемых пар:
   $$\vec{M}=\sum_{i=1}^{i=n}\vec{M_i}$$
2. Система n пар на плоскости эквивалентна одной паре с моментом, равным алгебраической сумме моментов слагаемых пар:
   $$M=\sum_{i=1}^{i=n}M_i$$

В соответствии с замечанием в конце предыдущего параграфа вектор-момент пары сил в пределах рассматриваемого тела, как в математике, является свободным, поэтому последняя теорема может показаться излишней.

В действительности между векторами в математике и векторами в ТМ продолжает оставаться различие, которое обнаруживается при рассмотрении системы аксиом, которым удовлетворяют векторы в математике и не удовлетворяют вектора сил.