Частные случаи приведения плоской системы сил
В зависимости от значений главного вектора $\vec{R_0}$ и главного момента $\vec{M_0}$ возможны следующие случаи приведения плоской системы сил.
- $R_0 = 0,\, M_0 = 0$ – система сил находится в равновесии;
- $R_0 = 0,\, M_0 \neq 0$ – система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения;
- $R_0 \neq 0,\, M_0 = 0$ – система эквивалентна равнодействующей $\vec{R}$ ,равной и эквивалентной главному вектору системы $\vec{R_0}$ , линия действия которой проходит через центр приведения: $\vec{R} = \vec{R_0} , \vec{R} \sim \vec{R_0}$ ;
- $R_0 \neq 0,\, M_0 \neq 0$ – система эквивалентна равнодействующей $\vec{R}$, равной главному вектору системы $\vec{R_0}$ , ее линия действия проходит на расстоянии $d = \frac{|M_0|}{R_0}$ от центра приведения.
Чтобы убедиться в этом, достаточно рассмотреть доказательство леммы Пуансо в обратном направлении, сменив силу $\vec{P}$ на $\vec{R}$, а $\vec{P'}$ – на $\vec{R_0}$ .
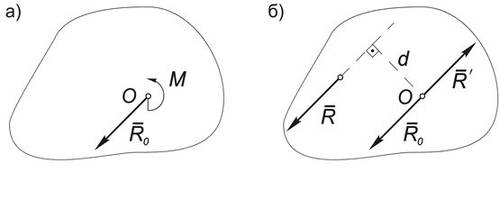
В самом деле, пусть система эквивалентна главному вектору $\vec{R_0}$ и главному моменту $\vec{M_0}$ (Рис.1а). Заменим $\vec{M_0}$ парой сил $(\vec{R}, \vec{R'})$ с моментом $M(\vec{R}, \vec{R'}) = М_0$ , выбрав силы пары равными по модулю и параллельными $\vec{R_0}$ , а ее плечо $d = \frac{|M_0|}{R_0} $ (Рис.1б). Тогда
$$(\vec{R_0}, \vec{M_0}) \sim (\vec{R_0}, (\vec{R}, \vec{R'})) \sim (\vec{R}, (\vec{R_0}, \vec{R'}) \sim \vec{R}$$
, поскольку $(\vec{R_0}, \vec{R'}) \sim 0$ . Таким образом, система $(\vec{R_0}, \vec{M_0})$ действительно эквивалентна равнодействующей $\vec{R}$ , линия действия которой проходит на расстоянии $d = \frac{|M_0|}{R_0}$ от центра приведения.
Следствием этого случая приведения является
Теорема Вариньона (о моменте равнодействующей плоской системы сил).
Момент равнодействующей плоской системы сил относительно
произвольного центра О равен алгебраической сумме моментов всех сил системы
относительно этого центра.
Выбирая центр О, о котором идет речь в теореме, в качестве нового центра приведения системы сил, состоящей из единственной силы – равнодействующей $\vec{R}$ , и учитывая, что $R = R_0$ получим:
$$M_0(\vec{R}) = \pm R \cdot d = \pm R \cdot \frac{|M_0|}{R_0} = M_0 = \sum M_0 (\vec{P_i})$$