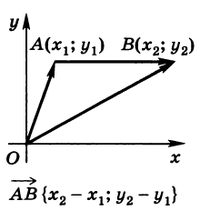Координаты вектора

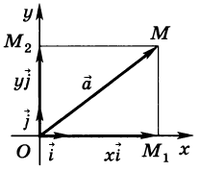
Обозначим через $\overrightarrow{i} \,и\, \overrightarrow{j}$ единичные векторы, отложенные от точки О в положительных направлениях на осях Ох и Оу прямоугольной системы координат (рис. 1).

Пусть $\overrightarrow{a}$ — любой вектор на плоскости хОу. Тогда вектор $\overrightarrow{a}$ можно представить в виде $$ \overrightarrow{a} = x \overrightarrow{i} + y \overrightarrow{j} \,\,\, (1)$$ и притом единственным образом.

Если вектор $\overrightarrow{a}$ представлен в виде $\overrightarrow{a} = x \overrightarrow{i} + у \overrightarrow{j}$ , то говорят, что $\overrightarrow{a}$ разложен по векторам $\overrightarrow{i} \,и\, \overrightarrow{j}$ . Векторы $\overrightarrow{a}_х = x \overrightarrow{i} \,и\, \overrightarrow{a}_у = у \overrightarrow{j}$ называют составляющими вектора $\overrightarrow{a}$ по осям Ох и Оу. Коэффициенты х и у разложения вектора $\overrightarrow{a}$ по единичным векторам $\overrightarrow{i} \,и\, \overrightarrow{j}$ называют координатами вектора $\overrightarrow{a}$ в данной системе координат и записывают $\overrightarrow{a}\{х;\, у\}\text{ . Тогда }|\overrightarrow{a}| = \sqrt{x^2 + у^2}$ .

Из единственности представления (1) следует, что равные векторы имеют равные соответствующие координаты, и обратно, если у векторов соответствующие координаты равны, то векторы равны.

Пусть дана точка М(х; у). Тогда $\overrightarrow{r} = \overrightarrow{ОМ} = x \overrightarrow{i} + y \overrightarrow{j}$ , где х и у — координаты точки М, т.е. $\overrightarrow{r}\{х;\, у\}, |\overrightarrow{r}| = \sqrt{x^2 + у^2}$ .

Теорема 1. Каждая координата суммы векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ равна сумме соответствующих координат этих векторов; каждая координата произведения вектора $\overrightarrow{a}$ на число k равна произведению соответствующей координаты этого вектора на число k.

Доказательство. Пусть $\overrightarrow{a} = x_1 \overrightarrow{i} + _1 \overrightarrow{j}\,\,,\, \overrightarrow{b} = x_2\overrightarrow{i} + y_2 \overrightarrow{j} $ .

Пользуясь свойствами сложения векторов и умножения вектора на число, получим $ \overrightarrow{a} + \overrightarrow{b} = (x_1 \overrightarrow{i} + y_1 \overrightarrow{j}) + (x_2 \overrightarrow{i} + y_2 \overrightarrow{j}) = (x_1 + x_2)\overrightarrow{i} + (y_1 + y_2)\overrightarrow{j} $ .

Аналогично доказывается: $ k\overrightarrow{a} = K(x_1 \overrightarrow{i} + y_1 \overrightarrow{j}) = (k x_1)\overrightarrow{i} + (k y_1)\overrightarrow{j} $ .

Значит, координаты вектора $\overrightarrow{a} + \overrightarrow{b}$ равны $х_1 + х_2$ и $у_1 + у_2$ , координаты вектора $k\overrightarrow{a}$ равны $kx_1 \,и\, ky_1$ . Теорема доказана.

Следствие 1. Координаты вектора $\overrightarrow{АВ}$ , заданного двумя точками $А(х_1; у_1) \,и\, В(х_2; у_2)$ , равны разностям соответствующих координат точек А и В.

Доказательство. Имеем $\overrightarrow{АВ} = \overrightarrow{ОВ} - \overrightarrow{ОА}$ (рис.2).

Так как $\overrightarrow{ОА}\{х_1; y_1\},\, \overrightarrow{ОВ}\{х_2; у_2\}$ , то по теореме 1: $\overrightarrow{АВ} \{х_2 - х_1;\, у_2 - у_1\}$ .

---

---

Пример 1. Найти координаты вектора $\overrightarrow{c} = \overrightarrow{a} - 3\overrightarrow{b}$ , если $\overrightarrow{a}\{3;2\},\,\overrightarrow{b}\{-3;1\}$ .

Решение. Согласно полученной теореме 1:
х = 3 - 3•(-3) = 12 ;
у = 2 - 3•1 = -1 .

---

Пример 2. Найти координаты вектора $\overrightarrow{a} = \overrightarrow{AB}$ , если А(1;3) и В(5;8).

Решение. Согласно следствию 1:
x = 5 - 1 = 4 ;
y = 8 - 3 = 5 .

---

---