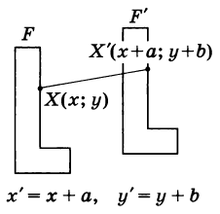-
- Подобие произвольных фигур
Подобие произвольных фигур
Понятие подобия можно ввести не только для треугольников, но и для произвольных фигур. Фигуры F и F1 называются подобными, если каждой точке фигуры F можно сопоставить точку фигуры F1 так, что для любых двух точек М и N фигуры F и сопоставленных им точек М1 и N1 фигуры F1 выполняется условие $\frac{M_1N_1}{MN} = k$ , где k — одно и то же положительное число для всех точек. При этом предполагается, что каждая точка фигуры F1 оказывается сопоставленной какой-то точке фигуры F. Число k называется коэффициентом подобия фигур F и F1.
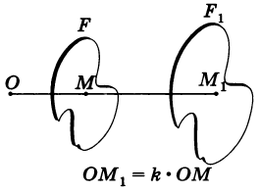
На рисунке 1 представлен способ построения фигуры F1 , подобной данной фигуре F. Каждой точке М фигуры F сопоставляется точка М1 плоскости так, что точки М и М1 лежат на луче с началом в некоторой фиксированной точке О, причем ОМ1 = k*OM (на рис.1 k = 3). В результате такого сопоставления получается фигура F1, подобная фигуре F.
Этот способ построения фигуры F1, подобной фигуре F, называется центрально-подобным преобразованием фигуры F в фигуру F1 или гомотетией, а фигуры F и F1 — центрально-подобными или гомотетичными.
Можно доказать, что для треугольников общее определение подобия равносильно определению, данному в п.1.
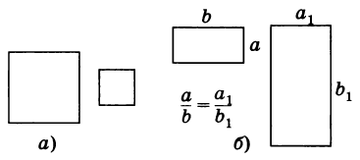
Примерами подобных четырехугольников являются любые два квадрата (рис. 2, а), а также два прямоугольника, у которых две смежные стороны одного пропорциональны двум смежным сторонам другого (рис. 2, б).
Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.
Гомотетия и рассмотренные ранее центральная симметрия и осевая симметрия — примеры преобразований фигур.
Рассмотрим еще один пример преобразования фигуры — параллельный перенос.
Преобразование фигуры F, при котором каждая ее точка Х(х; у) переходит в точку Х'(х + а; у + b), а и b постоянные, называется параллельным переносом (рис.3).
Параллельный перенос задается формулами $$ x' = x + a \\ y' = y + b $$ Эти формулы выражают координаты х', у' точки, в которую переходит точка (х; у) при параллельном переносе.
Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
Заметим также, что при параллельном переносе прямая переходит в параллельную прямую (или в себя).
Пример 1. При параллельном переносе точка (1; 1) переходит в точку (-1; 0). В какую точку переходит начало координат?
Решение. Любой параллельный перенос задается формулами х' = х + а; у' = у + b. Так как точка (1; 1) переходит в точку (-1; 0), то -1 = 1 + а; 0 = 1 + b. Отсюда а = -2 ; b = -1.
Таким образом, параллельный перенос, переводящий точку (1; 1) в (-1; 0), задается формулами х' = х - 2 ; у' = у - 1.
Подставляя в эти формулы координаты начала (х = 0; у = 0), получим: х' = -2; у' = -1.
Итак, начало координат переходит в точку (-2; -1).
| ← Признаки подобия треугольников | Геометрия ( Справочник ) | Касательная к окружности → |
|---|---|---|
| Рекомендуем для обучения: | ||
| Примеры центральной симметрии | ||