Аналитическое задание силы

Термин «аналитический» в механике, как и в аналитической геометрии, означает применение системы координат при решении той или иной проблемы.

Определение. Проекцией силы $\vec{Р}$ на ось Ox называется взятая с знаком $\pm$ длина отрезка этой оси, заключенная между проекциями на неё начала и конца вектора силы.

Эту проекцию обычно обозначают как Р_x или X. В соответствии с определением она равна:

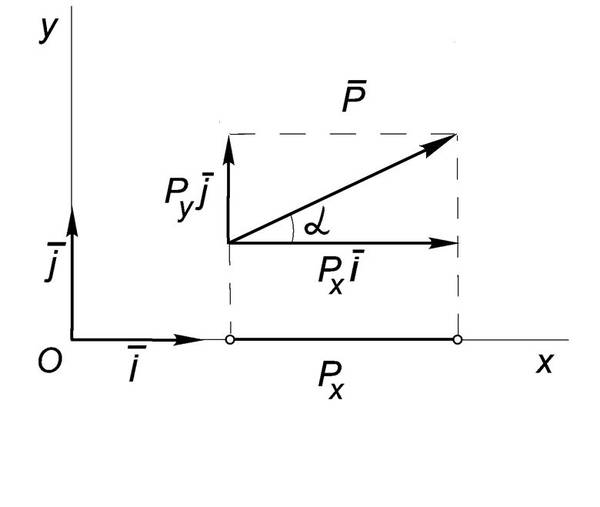
$$ P_x = X = |\vec{Р}| \cdot \cos (\vec{Р}, \vec{i}) = P \cdot \cos \alpha = (\vec{Р} \cdot \vec{i})$$

, где $\vec{i}$ – единичный вектор оси /Ox/, а $\alpha$ – угол между ним и силой $\vec{Р}$ (Рис.1).

Таким образом: $$ P_x \left\{\begin{matrix} > 0\text{, если }0 \leq \alpha < \frac{\pi}{2} \\ = 0\text{, если } \alpha = \frac{\pi}{2} \\ < 0\text{, если } \frac{\pi}{2} < \alpha \leq \pi \end{matrix}\right. $$

Аналогично находится проекция силы Р на ось Oy.

Если проекцию силы на какую-либо ось умножить на орт этой оси, мы получим векторную величину, которая равна составляющей силы вдоль этой оси. Очевидно, сила $\frac{\pi}{2}$ является равнодействующей по отношению к своим составляющим, поэтому в соответствии с теоремой:

$$\vec{Р} = P_x \cdot \vec{i} + P_y \cdot \vec{j} = X \cdot \vec{i} + Y \cdot \vec{j}$$

Поставим следующую задачу. Пусть известны проекции силы на оси координат – X,Y,Z и координаты точки приложения этой силы – A(x,y,z), а нужно определить вектор силы $\vec{Р}$.

Для ее решения построим прямоугольный параллелепипед с вершиной в точке А и со сторонами, равными соответственно X,Y,Z. При этом будем откладывать отрезок длиной X в положительном направлении оси, если X>0 и в противоположном направлении, – если X<0.

Умножая каждую из проекций на орт соответствующей оси, найдем составляющие искомой силы вдоль координатных осей, которые образуют систему сходящихся сил с центром в точке А. Равнодействующая этой системы, согласно теореме, будет также приложена в точке А и равна вектору:

$$\vec{Р} = X \cdot \vec{i} + Y \cdot \vec{j} + Z \cdot \vec{k}$$

Таким образом, равнодействующая пространственной системы трех сходящихся сил изображается диагональю параллелепипеда, построенного на этих силах, как на сторонах.

Модуль и направление искомого вектора силы Р можно найти по формулам:

$$ P = \sqrt{X^2 + Y^2 + Z^2} \\ \cos (\vec{Р}, \vec{i}) = \frac{X}{P} \\ \cos (\vec{Р}, \vec{j}) = \frac{Y}{P} \\ \cos (\vec{Р}, \vec{k}) = \frac{Z}{P} $$