Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников вытекает следствие.
Следствие 1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Далее, из второго признака равенства треугольников вытекает следствие.
Следствие 2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Рассмотрим еще два признака равенства прямоугольных треугольников.
Теорема 1. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Доказательство. Из следствия 1 следует, что в таких треугольниках два других острых угла также равны, поэтому треугольники равны по второму признаку равенства треугольников. Теорема доказана.
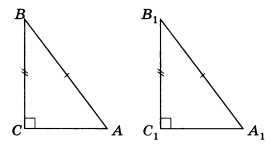
Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны (рис.1).
Пример 1. Доказать, что каждая точка биссектрисы угла равноудалена от его сторон.
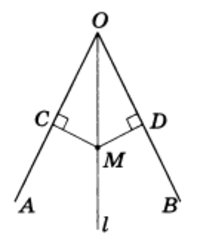
Решение. Пусть l — биссектриса ∠ АОВ (рис.2).
Рассмотрим произвольную точку М, лежащую на луче l. Опустим из точки М перпендикуляры МС и MD на стороны угла АОВ. Прямоугольные треугольники ОМС и OMD равны по теореме 1: у них гипотенуза ОМ общая, а углы СОМ и DOM равны по условию. Отсюда следует, что МС = MD.
Пример 2. Доказать, что точка плоскости, равноудаленная от сторон угла, лежит на биссектрисе этого угла.
Решение. Пусть точка М равноудалена от сторон угла АОВ (см. рис.3), т. е. перпендикуляры МС и MD к сторонам угла равны.
Тогда Δ ОМС = Δ OMD по теореме 2. Отсюда ∠ СОМ = ∠ DOM, и, следовательно, луч ОМ является биссектрисой угла АОВ.
Замечание. Предложения, установленные в примерах 1 и 2 выражают свойства биссектрисы угла. Из этих предложений следует, что биссектрисы треугольника пересекаются в одной точке.
Пример 3. Доказать, что в прямоугольном треугольнике с углом 30° катет, противолежащий этому углу, равен половине гипотенузы.
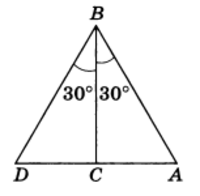
Решение. Пусть ABC — прямоугольный треугольник с прямым углом С и острым углом В, равным 30° (рис.3).
Отложим на продолжении стороны АС отрезок CD, равный АС.
Прямоугольные треугольники АСВ и DCB (углы при вершине С прямые) равны по двум катетам (сторона ВС общая, а АС = CD по построению).
Из равенства треугольников следует, что ∠ D = ∠ А = 60°, ∠ CBD = ∠ CBA = 30°, а значит, ∠ ABD= 60°. Отсюда следует, что треугольник ABD равносторонний. Поэтому АС = 1/2 * AD = 1/2 * АВ, что и требовалось доказать.